4 Working with Graphs in a Relational Database
4.1 Data Structures
The lack of advanced data types and flexible program control greatly reduces the number of viable graph representations in a relational database. The edge list data structure is the de facto standard. It is introduced in Section 4.1.1. Section 4.1.2 presents an attempt to create an adjacency matrix in a relational database.
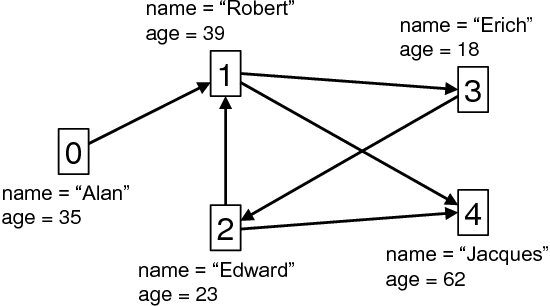
The social network graph shown below is
used as an example in this chapter. Vertices represent people and edges mark
who-knows-whom. Each vertex is labeled with a unique identifier, a person’s
name, and his age. Edges are not labeled and parallel edges and loops are not
allowed.
4.1.1 Edge List
The edge list data structure is the de facto standard for storing graphs in a relational database. It is the database equivalent of the unordered edge list (see Section 3.1.1). Since a table in a relational database by definition stores an unordered set of records, the term “unordered” is redundant.
Several aspects should be considered when setting up the data structure: First, to comply with the domain/key normal form, vertex labels should be represented separately from edges. If vertex labels and edges were represented in the same table, complex constraints would be necessary to enforce data consistency.
The primary key for the vertices table is the unique vertex identifier. The edges table has two columns holding foreign keys. Since parallel edges are not allowed in the example graph, the columns can be a joined primary key for the edges table. Additionally, this prevents the user from illegally inserting an edge that already exists in the graph. We should add another constraint to prevent the insertion of loops.
Finally, both tables should be properly supported by indexes. Most database management systems (DBMSs) automatically create indexes on primary key columns to enforce primary key uniqueness. To speed up graph navigation, an index on each column of the edges relation should be added. To speed up the creation of the graph, it is advisable to add the indexes after the table has been filled.
In PostgreSQL, the data structure can be created as follows.
CREATE TABLE vertices( id INTEGER PRIMARY KEY, name VARCHAR(20), age SMALLINT); CREATE TABLE edges( a INTEGER NOT NULL REFERENCES vertices(id), b INTEGER NOT NULL REFERENCES vertices(id), PRIMARY KEY (a, b), CONSTRAINT no_loops CHECK (a != b)); CREATE INDEX idx_a ON edges(a);CREATE INDEX idx_b ON edges(b);
After inserting the example social network, finding who in the network is known to ‘Robert’ is a simple task:
Output A B ID NAME AGE
1 3 3 Erich 18 1 4 4 Jacques 62 SELECT * FROM edges JOIN vertices ON b = idWHERE a = (SELECT id FROM vertices WHERE name = 'Robert');
4.1.2 Relational Adjacency Matrix
The relational adjacency matrix is an attempt to create an adjacency matrix (see Section 3.1.4) in a relational database. Just like a matrix, a table in a relational database consists of rows and columns. The only structural difference is that the rows in a database table are identified by primary keys, which can have an arbitrary type and value, while the rows in a matrix are identified by consecutive integers. We can overcome this difference by choosing appropriate primary keys.
There a several aspects to consider: First,
since it is not possible in SQL to select columns based on values in rows, we
should transpose the adjacency matrix. In other words, all edges incident on
vertex ![]() should be stored
in column
should be stored
in column ![]() instead of in
row
instead of in
row ![]() .
.
Second, some DBMSs, including Oracle, do not supply a data type for representing booleans. In such systems, a CHAR(1) type constrained to ‘0’ and ‘1’ can be used. PostgreSQL does supply a boolean type, BOOLEAN. It uses one byte of storage.
Finally, most s limit the number of columns a table can have. PostgreSQL’s limit lies between 250 and 1600, depending on the types of the columns. Oracle’s limit is 1000. As a solution, we suggest storing several columns of the matrix in a character string, and using string functions to filter for a specific column. If the SQL function SUBSTR() is implemented efficiently, an individual character in a character string can be accessed in constant time.
Which data type to use depends on the DBMS and the size of the graph. PostgreSQL’s TEXT data type can store character strings of unlimited length. Oracle’s VARCHAR data type can store up to 4000 characters. Oracle’s CLOB (“Character Large Object”) data type can store up to 4 GB of text. This data type has special string functions (e.g., DBMS_LOB.SUBSTR()).
Experiments should determine if the columns of the adjacency matrix are better represented in one large column or in multiple smaller columns. To create a data structure for the example graph, we use a single column and PostgreSQL’s TEXT data type:
CREATE TABLE adjmat( id INTEGER PRIMARY KEY, cols TEXT); --01234INSERT INTO adjmat VALUES(0,'00000');INSERT INTO adjmat VALUES(1,'10100'); --(0,1), (2,1)INSERT INTO adjmat VALUES(2,'00010'); --(3,2)INSERT INTO adjmat VALUES(3,'01000'); --(1,3)INSERT INTO adjmat VALUES(4,'01100'); --(1,4), (2,4)
The following query finds the neighbors of ‘Robert’:
Output ID COLS NAME AGE
3 01000 Erich 18 4 01100 Jacques 62 SELECT * FROM adjmat NATURAL JOIN verticesWHERE SUBSTR(cols, 1 + (SELECT id FROM vertices WHERE name = 'Robert'), 1) = '1';
The relational adjacency matrix is an experimental data structure. Since it does not rely on joins for graph navigation, we think that it may have the potential to perform better than the edge list data structure in some applications. Procedural language extensions for SQL may have to be used to take advantage of the relational adjacency matrix’ capabilities.
4.2 Queries
In this section, we present four approaches for traversing a graph stored in an edge list data structure in a relational database. In main memory, we could utilize the manifold functionality of modern programming languages. In a relational database, we are bound to the functionality of SQL and the DBMS. The example queries in this section have been created in PostgreSQL 8.4, except where stated otherwise.
4.2.1 Breadth-First with Joins
The simplest way to navigate breadth-first in a graph is to repeatedly join the edges relation on itself. Every join corresponds to a run of the outermost for loop in the BFS algorithm presented in Section 3.2.1. With a single join, vertices at level 2 are reached. With two joins, vertices at level 3 are reached, and so on. The query below shows how joins can be used to find a list of people known to people known to ‘Robert’. The columns A A B contain the identifiers of the vertices along the paths.
Output ID NAME AGE A A B
2 Edward 32 1 3 2 SELECT * FROM vertices JOIN (SELECT lvl_1.a, lvl_2.a, lvl_2.b FROM edges lvl_1 JOIN edges lvl_2 ON lvl_1.b = lvl_2.a WHERE lvl_1.a = (SELECT id FROM vertices WHERE name = 'Robert')) lvl_2 ON id = lvl_2.b;
The query returns a list of people at the target level. The query below includes each person along each path. A person’s name is padded with spaces according to his level in the path. The three common table expressions (WITH ...) are used to prevent the DMBS from retrieving the same path multiple times, and to make the query more readable.
Output NAME AGE
Robert 39 Erich 18 Jacques 62 Edward 32 WITH lvl_1 AS (SELECT id FROM vertices WHERE name = 'Robert'), lvl_2 AS (SELECT b FROM edges WHERE a = (SELECT * FROM lvl_1)), lvl_3 AS (SELECT b FROM edges WHERE a IN (SELECT * FROM lvl_2)) SELECT LPAD(' ', lvl) || name AS name, age FROM (SELECT 0 lvl, name, age FROM vertices WHERE id = (SELECT * FROM lvl_1) UNION ALL SELECT 1 lvl, name, age FROM vertices WHERE id IN (SELECT * FROM lvl_2) UNION ALL SELECT 2 lvl, name, age FROM vertices WHERE id IN (SELECT * FROM lvl_3)) q ORDER BY lvl;
Notice how the order of the output rows might lead us to believe that ‘Robert’ was connected to ‘Edward’ through ‘Jacques’. DFS can find a list with a more intuitive order, as we shall see below.
When navigating short distances in a graph, manual joins may well be used. For larger distances, queries with manual joins become very large and error-prone. One solution is to install a temporary table that holds frequently visited paths or the transitive closure of the graph. A disadvantage of such a table is that it has to be maintained and may use a considerable amount of space. Materialized views may mitigate the maintenance issue. Transitive reduction [1] may help to reduce the size of such a table.
4.2.2 Breadth-First with Recursive CTEs
Recursive common table expressions (CTEs) are a relatively new feature in the SQL standard. PostgreSQL added support in version 8.4, Oracle in version 11g. Strictly speaking, recursive CTEs implement iteration not recursion, and Oracle’s version of recursive CTEs also does not use the keyword RECURSIVE.
A recursive CTE consists of two parts, separated by a UNION or UNION ALL. The first part generates the initial set of rows. The second part is the recursive term and can contain a reference to its own output. The query below shows how a recursive CTE can be utilized to find all paths in the example graph. Notice the mechanism that prevents the query from falling into an infinite recursion:
Output ROOT DEST LEN PATH CYCLE
0 1 1 {0,1} f 0 1 4 {0,1,3,2,1} t 0 2 3 {0,1,3,2} f 0 3 2 {0,1,3} f 0 4 2 {0,1,4} f 0 4 4 {0,1,3,2,4} f 1 1 3 {1,3,2,1} t 1 2 2 {1,3,2} f ... (21 rows in total) WITH RECURSIVE all_paths(root, dest, len, path, cycle) AS( SELECT a, b, 1, ARRAY[a] || b, FALSE FROM edges UNION ALL SELECT root, b, len + 1, path || b, b = ANY(path) FROM edges JOIN all_paths ON a = dest WHERE NOT cycle) SELECT * FROM all_pathsORDER BY root, dest, len;
When the ORDER BY clause is omitted, the query returns output rows in non-decreasing order of LEN. Although SQL does not guarantee any order without ORDER BY, the natural order of the output is often an indication of how a query is executed by the DBMS. In this case, it is an indication of BFS.
The following query solves the single-source shortest path problem:
SELECT root, dest, MIN(len), path, cycle FROM all_pathsGROUP BY root, dest, path, cycleORDER BY root, dest;
To find paths for a specific source vertex, a WHERE filter can be added in the first part of the recursive CTE. If the filter is added outside of the CTE, the DBMS could retrieve all paths first, and then filter for the specified source vertex.
To limit the search to paths of a given length, a WHERE filter can be added in the second part of the recursive CTE. Again, if the filter is added outside of the CTE, the DBMS could apply it after retrieving all paths.
We are not aware of a technique to stop a recursive CTE as soon as a path has been found. This would be useful for answering reachability queries or shortest path queries in large graphs.
The query below finds all paths between ‘Alan’ and ‘Jacques’ with a length of at most 3. Notice how this query is more portable than the previous query, as it does not use the PostgreSQL-specific data types ARRAY and BOOLEAN:
Output ROOT DEST LEN PATH CYCLE
0 4 2 -0-1-4 0 WITH RECURSIVE all_paths(root, dest, len, path, cycle) AS( SELECT a, b, 1, '-' || a || '-' || b, '0' FROM edges WHERE a = (SELECT id FROM vertices WHERE name = 'Alan') UNION ALL SELECT root, b, len + 1, path || '-' || b, CASE WHEN path LIKE '%-' || b || '%' THEN '1' ELSE '0' END FROM edges JOIN all_paths ON a = dest WHERE NOT cycle = '1' AND len + 1 <= 3) SELECT * FROM all_pathsWHERE dest = (SELECT id FROM vertices WHERE name = 'Jacques')
4.2.3 Depth-First with PL/pgSQL
Depth-first traversal is more difficult in a relational database. In this section, we present a recursive approach based on PL/pgSQL, PostgreSQL’s procedural extension language for SQL. PL/pgSQL is very similar to PL/SQL, Oracle’s procedural SQL extension, and the functions shown in this section can be easily converted.
Similar to the C++ implementation presented in Section 3.2.2, the PL/pgSQL implementation consists of two functions: An initialization function dfs(), and a recursive function dfs1(). The functions use two additional database tables: A results table that must be created by the user, dfs_results, and a cycle detection table that is automatically created and deleted, dfs_tmp.
The structure of dfs_result depends on the purpose of DFS. To find a hierarchical list of people that can be reached from a given person in the example social network, dfs_result can be created as follows:
CREATE TABLE dfs_result( rownum SERIAL, id INTEGER NOT NULL REFERENCES vertices(id), level INTEGER, cycle BOOLEAN);
SERIAL is an integer data type in PostgreSQL that is automatically incremented with each new record in a table. We use it to keep track of the order in which records are inserted.
SELECT dfs(1); starts the search for source vertex ‘Robert’. 1 is the unique identifier for ‘Robert’. After the function returns, the user has to join dfs_results on the vertices table:
Output NAME AGE CYCLE
Robert 39 f Erich 18 f Edward 32 f Jacques 62 f Robert 39 t Jacques 62 f SELECT LPAD(' ', level) || name AS name, age, cycle FROM dfs_result NATURAL JOIN vertices ORDER BY rownum;
The list has an intuitive order. It tells us, for instance, that ‘Jacques’ is connected to ‘Robert’ both directly and through ‘Erich’ and ‘Edward’. The PL/pgSQL functions are:
CREATE FUNCTION dfs1(me int, lvl int) RETURNS void AS $$DECLARE c RECORD;BEGIN UPDATE dfs_tmp SET active = TRUE WHERE id = me; FOR c IN SELECT b, active FROM edges JOIN dfs_tmp ON b = id WHERE a = me LOOP IF c.active = TRUE THEN INSERT INTO dfs_result (id, level, cycle) VALUES (c.b, lvl + 1, TRUE); ELSE INSERT INTO dfs_result (id, level, cycle) VALUES (c.b, lvl + 1, FALSE); PERFORM dfs1(c.b, lvl + 1); END IF; END LOOP; UPDATE dfs_tmp SET active = FALSE WHERE id = me;END;$$ LANGUAGE plpgsql; CREATE FUNCTION dfs(s int) RETURNS void AS $$BEGIN DELETE FROM dfs_result; CREATE TABLE dfs_tmp AS SELECT id, FALSE active FROM vertices; INSERT INTO dfs_result (id, level, cycle) VALUES (s, 0, FALSE); PERFORM dfs1(s, 0); DROP TABLE dfs_tmp;END;$$ LANGUAGE plpgsql;
4.2.4 Depth-First with CONNECT BY
The CONNECT BY clause is an SQL extension for depth-first tree and graph traversal in Oracle and EnterpriseDB databases. Before recursive CTEs were introduced, it was by far the most convenient method for navigating in graphs stored in a relational database. The query below has been created in an Oracle 11g databases and shows how CONNECT BY can be used to find all paths with source ‘Robert’.
Output S D NAME A C L PATH
1 3 Erich 18 0 0 Robert-Erich 1 2 Edward 32 0 0 Robert-Erich-Edward 1 1 Robert 39 1 1 Robert-Erich-Edward-Robert 1 4 Jacques 62 0 1 Robert-Erich-Edward-Robert-Jacques 1 4 Jacques 62 0 1 Robert-Erich-Edward-Jacques 1 4 Jacques 62 0 1 Robert-Jacques SELECT CONNECT_BY_ROOT a s, b d, LPAD(' ', LEVEL) || name name, age a, CONNECT_BY_ISCYCLE c, CONNECT_BY_ISLEAF l, 'Robert' || SYS_CONNECT_BY_PATH(name, '-') path FROM edges JOIN vertices ON b = idSTART WITH a = (SELECT id FROM vertices WHERE name = 'Robert')CONNECT BY NOCYCLE PRIOR b = a;
Documentation of the clause and its associated pseudocolumns is included with every Oracle database. Notice the CONNECT_BY_ISLEAF pseudocolumn. It shows ‘1’ if no unexplored vertex is found during the scan of the neighborhood of a vertex.
Compare the output of this query with the output of the PL/pgSQL query in the previous section. Notice how the PL/pgSQL query stopped when it detected a cycle in path Robert-Erich-Edward-Robert, while the CONNECT BY query continued and found path Robert-Erich-Edward-Robert-Jacques.
To our knowledge, it is not possible to limit the traversal depth of a CONNECT BY query in Oracle. A WHERE condition on the LEVEL pseudocolumn is evaluated after traversal. This is different in G-Store’s query engine.